迪杰斯特拉算法
算法
- 初始化距离向量 d(长度为 V ),起点设为0,其他点设为无穷大
- 初始化集合 Q,含义为尚未确定距离的顶点的集合,将所有顶点加入
- 从 Q 中弹出距离最小的顶点 u
- 遍历 u 的所有仍在 Q中的邻居 w , 判断 d[u] + length(u,w) < d[w]是否成立,如果成立,更新d[w] = d[u] + length(u,w), 否则无视
- 回到 3 开始循环,直到 Q为空集
时间复杂度
- 初始化 d 和 Q 均为 O(V)
- 外层循环,每次删除一个顶点,共 V 个顶点,故为O(V)
- 内层 Extrac-min 为O(V),遍历邻居为 O(N)(N 为每个节点最大的邻居数)
综上,复杂度为 O(V) + O(V^2) + O(VN) ~O(V^2)
优化
时间复杂度依赖于最小优先队列的实现方式,如果用数组存储最小优先队列的话,时间复杂度才是O(V^2),因为每次调用extractmin都要遍历整个数组
图实现
如我们现在有如下有向加权图:
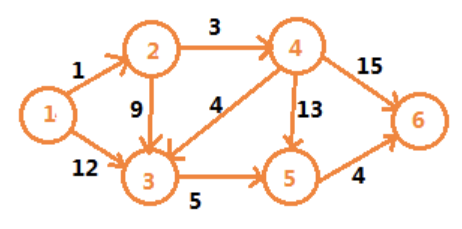
计算点 A 到其他顶点的最短距离。
同样的,我们创建 vertexes 数组来临时保存点 A 到其他顶点的最短路距离。在算法计算过程中,从点 A 开始往其他顶点扩散遍历。同时以当前遍历到的边结合 vertexes 数组中的值,不断更新 vertexes 数组中的值。
首先我们以邻接表来表示这个图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class Graph {
private class Edge {
public int sid;
public int tid;
public int w;
public Edge(int s, int t, int w) {
this.sid = s;
this.tid = t;
this.w = w;
}
}
private class Vertex {
public int id;
public int dist;
public Vertex(int id; int dist) {
this.id = id;
this.dist = dist;
}
}
private LinkedList<Edge> adj[];
private int v;
public Graph(int v) {
this.v = v;
this.adj = new LinkedList[v];
for(int i; i<v; i++) {
this.adj[i] = new LinkedList<Edge>();
}
}
public void addEdge(int s, int t, int w) {
this.adj[s].add(new Edge(s, t, w));
}
}
|
简单的说明一下这个类,它可以用来表示一张图,类中分别有两个成员变量表示邻接表和顶点数,其中,Edge 类表示一条边,结合邻接表可以将图的信息记录,Vertex 类则是记录起始节点到当前节点的最短距离。
在算法实现过程中,我们会使用一个优先队列,将离起始节点最近的节点优先出队,利用这个节点能到达的节点的距离与当前记录在 vertexes 数组中的最短距离比较,进行更新最短距离(松弛)。文字说的不太清楚,结合代码会更容易理解。
注意:由于 Java 类库中没有提供可更新节点信息的优先队列,因此我们需要手动实现一个优先队列,思路是使用一个小顶堆来实现。
优先队列代码实现
优先队列代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
|
private class PriorityQueue {
private Vertex[] nodes;
private int count;
public PriorityQueue(int v) {
this.nodes = new Vertex[v + 1];
this.count = 0;
}
public Vertex poll() {
Vertex v = this.nodes[1];
this.nodes[1] = this.nodes[count--];
heapify();
return v;
}
public void add(Vertex vertex) {
nodes[++this.count] = vertex;
int i = this.count;
while(i/2 > 0 && nodes[i/2].dist > nodes[i].dist) {
swap(i/2, i);
i = i/2;
}
}
public void update(Vertex vertex) {
for (int i = 1; i < count; i++) {
if (nodes[i].id == vertex.id) {
nodes[i] = vertex;
}
}
}
public boolean isEmpty() {
if (this.count != 0) {
return false;
} else {
return true;
}
}
private void heapify() {
int minPos = 1;
int temp = 1;
while (true) {
int left = temp * 2;
int right = temp * 2 + 1;
if (left <= count && nodes[left].dist < nodes[temp].dist) {
minPos = left;
}
if (right <= count && nodes[right].dist < nodes[minPos].dist) {
minPos = right;
}
if (minPos == temp) {
break;
}
swap(temp, minPos);
temp = minPos;
}
}
private void swap(int temp, int minPos) {
Vertex t = nodes[temp];
nodes[temp] = nodes[minPos];
nodes[minPos] = t;
}
}
|
现在,我们已经把所有的准备工作都做完了,剩下的只需要利用当前的条件来实现 Dijkstra 算法。
算法实现

从上图中顶点 1 开始遍历,顶点 1 可以连通到顶点 2 和 3,将顶点 2 和 3 入队,并同时在 vertexes 数组更新到达顶点 2 和 3 的距离。
接着出队为顶点 2,顶点 2 能连通的是顶点 3 和 4,此时,我们可以得到顶点 1 到 3 的距离是 1+9=10,而 vertexes 数组中记录的是 12,因此需要更新 vertexes 数组和队列中节点 3 的 dist 值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public void dijkstra(int s, int t) {
int[] pre = new int[this.v+1];
Vertex[] vertexes = new Vertex[this.v+1];
for(int i=0; i<this.v; i++) {
vertexes[i] = new Vertex(i, Integer.MAX_VALUE);
}
PriorityQueue queue = new PriorityQueue(this.v+1);
boolean[] inqueue = new boolean[this.v+1];
vertexes[s].dist = 0;
queue.add(vertexes[s]);
inqueue[s] = true;
while(!queue.isEmpty()) {
Vertex minVertex = queue.poll();
if(minVertex.id == t){
break;
}
for(int i=0; i<this.adj[minVertex.id].size(); i++){
Edge e = this.adj[minVertex.id].get(i);
Vertex nextVertex = vertexes[e.tid];
if(minVertex.dist + e.w < nextVertex.dist) {
nextVertex.dist = minVertex.dist + e.w;
pre[nextVertex.id] = minVertex.id;
if(inqueue[nextVertex.id]){
queue.update(nextVertex);
} else {
queue.add(nextVertex);
inqueue[nextVertex.id] = true;
}
}
}
}
System.out.print(s);
print(s, t, pre);
}
private void print(int s, int t, int[] pre) {
if(s == t) return;
print(s, pre[t], pre);
System.out.print("->"+t);
}
|
测试代码
测试代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public static void main(String[] args) {
Graph g = new Graph(6);
g.addEdge(1, 2, 1);
g.addEdge(1, 3, 12);
g.addEdge(2, 4, 3);
g.addEdge(2, 3, 9);
g.addEdge(4, 3, 4);
g.addEdge(4, 5, 13);
g.addEdge(3, 5, 5);
g.addEdge(5, 6, 4);
g.addEdge(4, 6, 15);
g.dijkstra(1, 6);
}
|
算法复杂度
Dijkstra 算法的核心逻辑已经讲完了,我们现在来考虑一下算法的复杂度情况。
在核心代码部分,最复杂的是 while 循环和 for 循环嵌套的部分,while 循环最多循环 v 次(v 为顶点个数),for 循环执行次数与边的数目有关,假设顶点数 v 的最大边数是 e。
for 循环中往优先队列中添加删除数据的复杂度为O(log v)。
综合上述两部分,最终 Dijkstra 算法的时间复杂度是O(e·logv)
为什么权重不能为负
Dijkstra算法是贪心算法,大概前提是,从当前的所有可能中就能找到全局的最优解,而负权图不满足这个条件(比如本文末尾的图例)
让我们从它的算法步骤上仔细分析一下
1
2
3
4
5
6
| 1.将图上的初始点看作一个集合S,其它点看作另一个集合
2.根据初始点,求出其它点到初始点的距离d[i] (若相邻,
则d[i]为边权值;若不相邻,则d[i]为无限大)
3.选取最小的d[i](记为d[x]),并将此d[i]边对应的点(记为x)加入集合S
4.再根据x,更新跟 x 相邻点 y 的d[y]值:d[y] = min{d[y], d[x] + 边权值w[x][y] },因为可能把距离调小,所以这个更新操作叫做松弛操作。
5.重复3,4两步,直到目标点也加入了集合,此时目标点所对应的d[i]即为最短路径长度。
|
在第三步中,若点 x 的 d[x] 值是最小的,就将此点加入集合,而这个 d[x] 便也就是 x 到初始点的最短距离了。
所以d[x]的确定尤其重要,而第三,四步中,d[x] 是根据已经处于集合中的点来更新的。
如果是正权图,集合内的点到初始点的最短距离已经确认了,把没在集合内的点加入路径只可能会增加无用的边,也就增加了路径长度;所以只根据集合内点的邻边来更新,就能得到当前的最小d[x]了。
但如果是负权图,注意上句话中的文字 “把没在集合内的点加入路径”,这个时候,如果边的长度是负的,就有可能产生更小的d[x]!而Dijkstra根本没有不会考虑 “把没在集合内的点加入路径”这种情况,这也就是Dijkstra算法目光短浅的原因。
这里有一个简单的例子:
从A到B的最短路。
用Dijkstra算法,第一步就能得到所谓的最短路径长度4,不会去考虑边(C,B)。
而实际上最短路径却需要加入边(C, B),长度是2。









