A-Star算法介绍

算法介绍

A*（念做：A Star）算法是一种很常用的路径查找和图形遍历算法。它有较好的性能和准确度。

A*算法最初发表于1968年，由Stanford研究院的Peter Hart, Nils Nilsson以及Bertram Raphael发表。它可以被认为是Dijkstra算法的扩展。

广度优先搜索

为了更好的理解A*算法，我们首先从广度优先（Breadth First）算法讲起。

正如其名称所示，广度优先搜索以广度做为优先级进行搜索。

从起点开始，首先遍历起点周围邻近的点，然后再遍历已经遍历过的点邻近的点，逐步的向外扩散，直到找到终点。

这种算法就像洪水（Flood fill）一样向外扩张，算法的过程如下图所示：

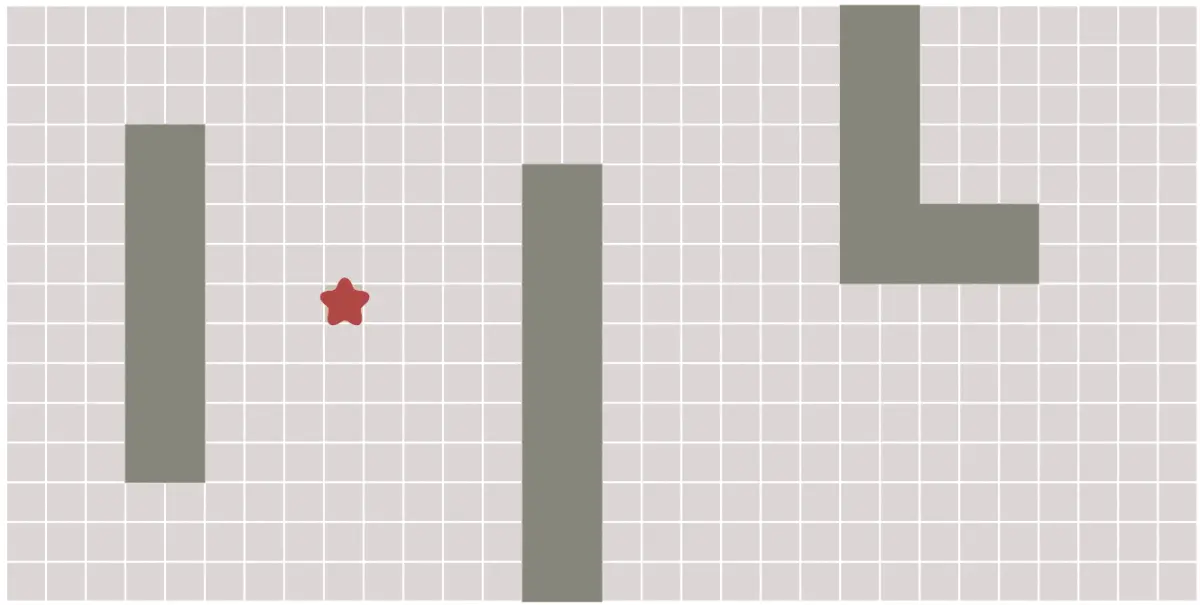
在上面这幅动态图中，算法遍历了图中所有的点，这通常没有必要。对于有明确终点的问题来说，一旦到达终点便可以提前终止算法，下面这幅图对比了这种情况：

在执行算法的过程中，每个点需要记录达到该点的前一个点的位置 — 可以称之为父节点。这样做之后，一旦到达终点，便可以从终点开始，反过来顺着父节点的顺序找到起点，由此就构成了一条路径。

Dijkstra算法

Dijkstra算法是由计算机科学家Edsger W. Dijkstra在1956年提出的。

Dijkstra算法用来寻找图形中节点之间的最短路径。

考虑这样一种场景，在一些情况下，图形中相邻节点之间的移动代价并不相等。例如，游戏中的一幅图，既有平地也有山脉，那么游戏中的角色在平地和山脉中移动的速度通常是不相等的。

在Dijkstra算法中，需要计算每一个节点距离起点的总移动代价。同时，还需要一个优先队列结构。对于所有待遍历的节点，放入优先队列中会按照代价进行排序。

在算法运行的过程中，每次都从优先队列中选出代价最小的作为下一个遍历的节点。直到到达终点为止。

下面对比了不考虑节点移动代价差异的广度优先搜索与考虑移动代价的Dijkstra算法的运算结果：

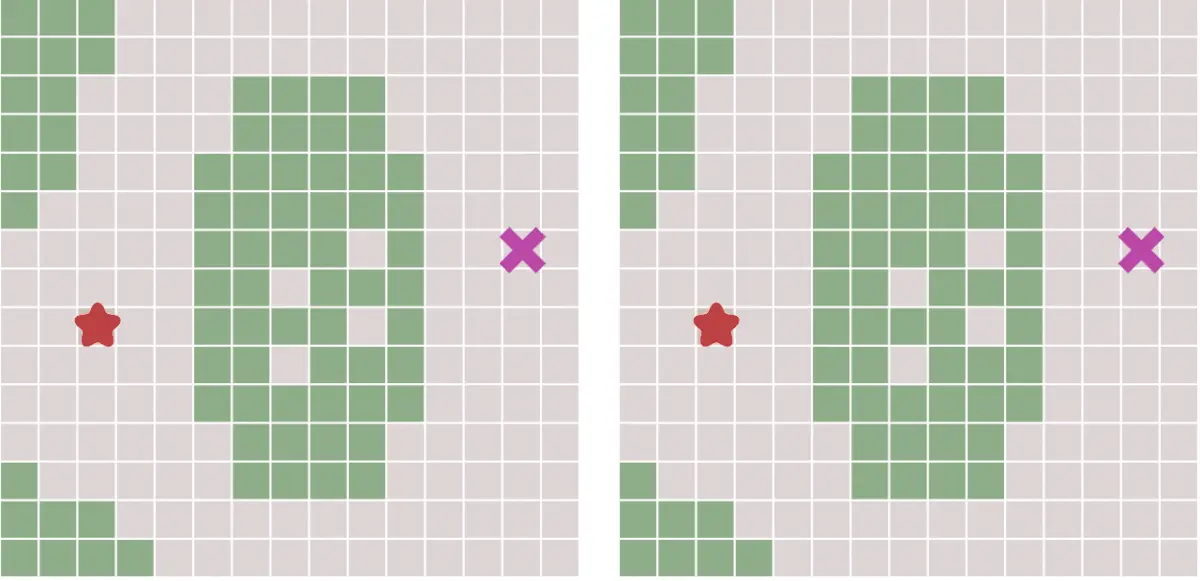
1
当图形为网格图，并且每个节点之间的移动代价是相等的，那么Dijkstra算法将和广度优先算法变得一样。

最佳优先搜索

在一些情况下，如果我们可以预先计算出每个节点到终点的距离，则我们可以利用这个信息更快的到达终点。

其原理也很简单。与Dijkstra算法类似，我们也使用一个优先队列，但此时以每个节点到达终点的距离作为优先级，每次始终选取到终点移动代价最小（离终点最近）的节点作为下一个遍历的节点。这种算法称之为最佳优先（Best First）算法。

这样做可以大大加快路径的搜索速度，如下图所示：

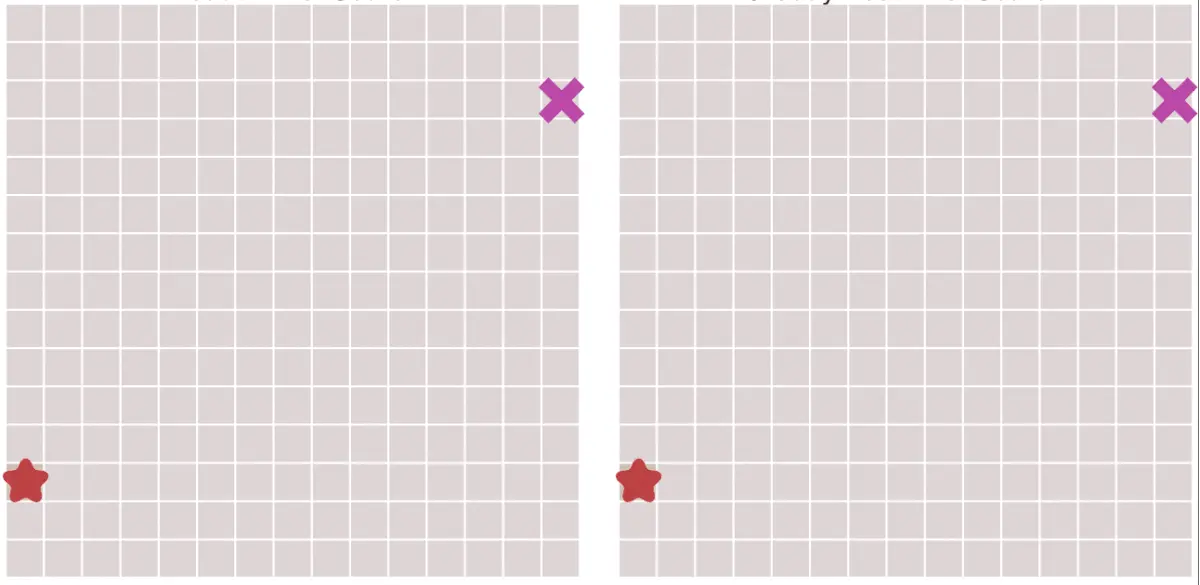
但这种算法会不会有什么缺点呢？答案是肯定的。

因为，如果起点和终点之间存在障碍物，则最佳优先算法找到的很可能不是最短路径，下图描述了这种情况。

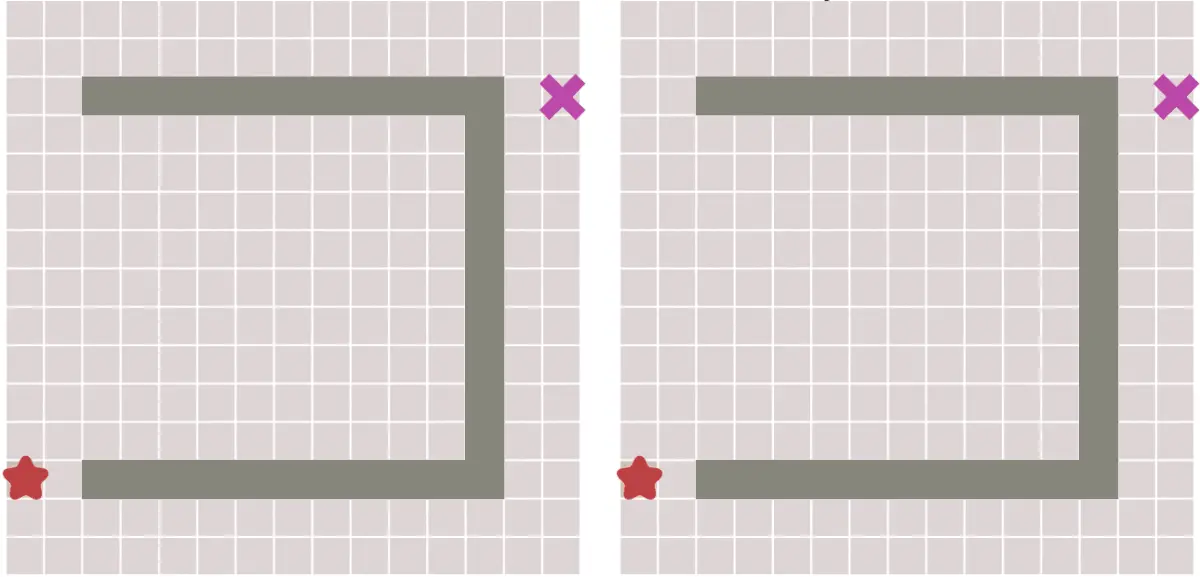
A*算法

对比了上面几种算法，最后终于可以讲解本文的重点：A*算法了。

下面的描述我们将看到，A*算法实际上是综合上面这些算法的特点于一身的。

A*算法通过下面这个函数来计算每个节点的优先级。

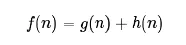
其中：

  • f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
  • g(n) 是节点n距离起点的代价。
  • h(n)是节点n距离终点的预计代价，这也就是A*算法的启发函数。关于启发函数我们在下面详细讲解。

A*算法在运算过程中，每次从优先队列中选取f(n)值最小（优先级最高）的节点作为下一个待遍历的节点。

另外，A*算法使用两个集合来表示待遍历的节点，与已经遍历过的节点，这通常称之为open_set和close_set。

完整的A*算法描述如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
* 初始化open_set和close_set；
* 将起点加入open_set中，并设置优先级为0（优先级最高）；
* 如果open_set不为空，则从open_set中选取优先级最高的节点n：
    * 如果节点n为终点，则：
        * 从终点开始逐步追踪parent节点，一直达到起点；
        * 返回找到的结果路径，算法结束；
    * 如果节点n不是终点，则：
        * 将节点n从open_set中删除，并加入close_set中；
        * 遍历节点n所有的邻近节点：
            * 如果邻近节点m在close_set中，则：
                * 跳过，选取下一个邻近节点
            * 如果邻近节点m也不在open_set中，则：
                * 设置节点m的parent为节点n
                * 计算节点m的优先级
                * 将节点m加入open_set中

启发函数

上面已经提到，启发函数会影响A*算法的行为。

  • 在极端情况下，当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就退化成了Dijkstra算法。
  • 如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
  • 如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
  • 如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。
  • 在另外一个极端情况下，如果h(n)相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。

由上面这些信息我们可以知道，通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况，我们可能未必需要最短路径，而是希望能够尽快找到一个路径即可。这也是A*算法比较灵活的地方。

对于网格形式的图，有以下这些启发函数可以使用：

  • 如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离（Manhattan distance）。
  • 如果图形中允许朝八个方向移动，则可以使用对角距离。
  • 如果图形中允许朝任何方向移动，则可以使用欧几里得距离（Euclidean distance）。

关于距离

曼哈顿距离

如果图形中只允许朝上下左右四个方向移动，则启发函数可以使用曼哈顿距离，它的计算方法如下图所示：

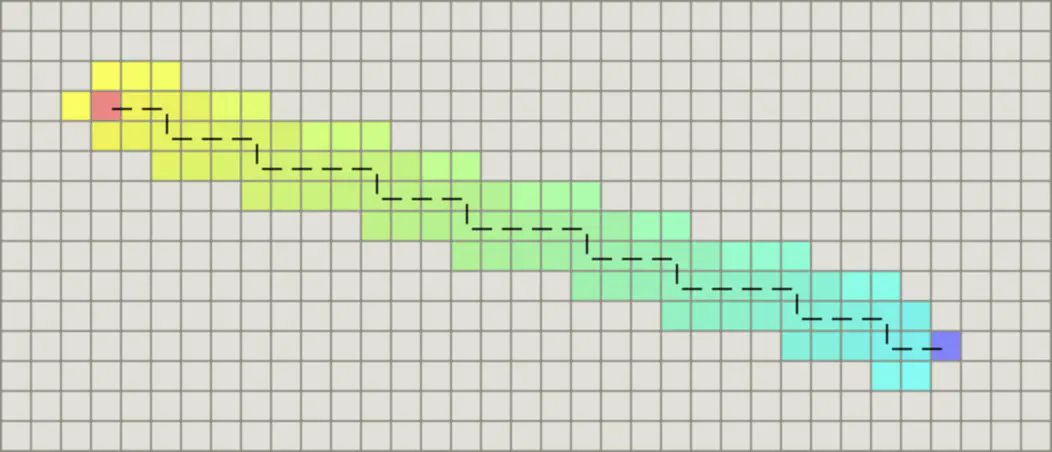
计算曼哈顿距离的函数如下，这里的D是指两个相邻节点之间的移动代价，通常是一个固定的常数。

1
2
3
4
function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy)

对角距离

如果图形中允许斜着朝邻近的节点移动，则启发函数可以使用对角距离。它的计算方法如下：

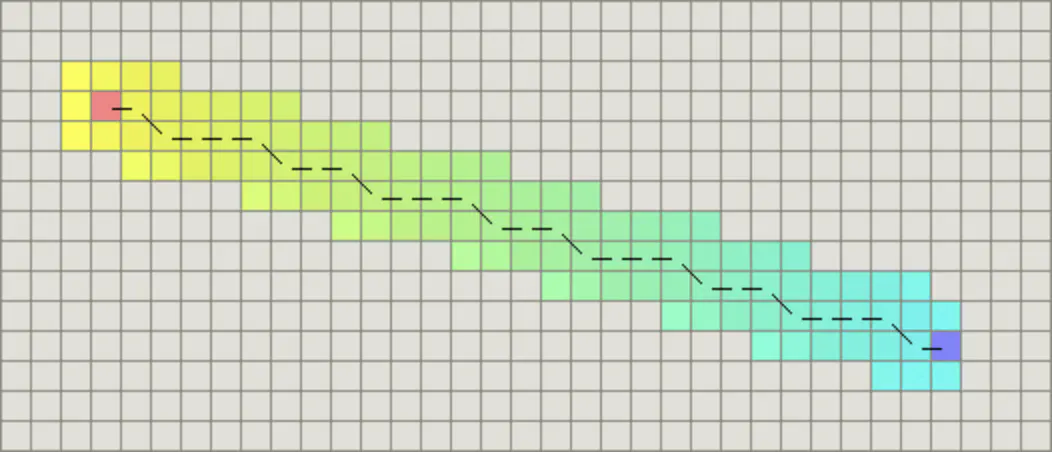
计算对角距离的函数如下，这里的D2指的是两个斜着相邻节点之间的移动代价。如果所有节点都正方形，则其值就是

1
2
3
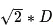
4
function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)

欧几里得距离

如果图形中允许朝任意方向移动，则可以使用欧几里得距离。

欧几里得距离是指两个节点之间的直线距离，因此其计算方法也是我们比较熟悉的：

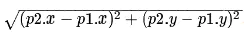
其函数表示如下：

1
2
3
4
function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * sqrt(dx * dx + dy * dy)