动态规划

力扣62题 不同路径

问题

一个机器人位于一个 m x n 网格的左上角。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。

问总共有多少条不同的路径？

力扣链接：https://leetcode-cn.com/problems/unique-paths

示例

1
2
3
4
5
6
7
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int uniquePaths(int m, int n) {
        //使用二维数组保存到当前位置的最大路径数
        int[][] dp = new int[m][n];        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0) {
                    //因为每次只能向下或向右移动，因此i==0或j==0时表示一直向右移动或一直向左移动，因此最大路径数都是1
                    dp[i][j] = 1;
                } else {
                    //只可能从(i-1,j)或(i,j-1)位置通过向下移动或向右移动到达当前(i,j)位置，所以到(i,j)的最大路径数等于前两个位置的最大路径数之和
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        //从左上角(0,0)点出发，不断利用上一步的结果动态更新下一个位置的最大路径数dp，最终更新完右下角dp[m-1][n-1]时，即可得出到达右下角的最大路径数
        return dp[m - 1][n - 1];        
    }
}

力扣376题 摆动序列

问题

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

力扣链接：https://leetcode-cn.com/problems/wiggle-subsequence

示例

1
2
3
输入: [1,7,4,9,2,5]
输出: 6 
解释: 整个序列均为摆动序列。
1
2
3
输入: [1,17,5,10,13,15,10,5,16,8]
输出: 7
解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return n;
        }
        //up(down)保存上一个以正数(负数)差值结尾的最长摆动序列子串长度,均初始化长度为1，表示开始时只有第一个数字
        int up = 1;
        int down = 1;
       
        //遍历数组，同时更新以正数、负数差值结尾的两个字符串的长度
        //假设当前位置i与i-1的差值为正，我们发现，无论上一个以负数差值结尾的最长子串的最后一位数字是不是位于i-1位置，我们都可以通过down+1来就表示新的以正数差值结尾的最长子串的长度up。见下图
        //因此我们每次只关心i与i-1的差值，并据此更新长度
        //i与i-1的差值为负时同理
        for (int i = 1; i < n; i++) {
            if (nums[i] > nums[i - 1]) {
                up = down + 1;
            }
            if (nums[i] < nums[i - 1]) {
                down = up + 1;
            }
        }
        return Math.max(up, down);
    }
}

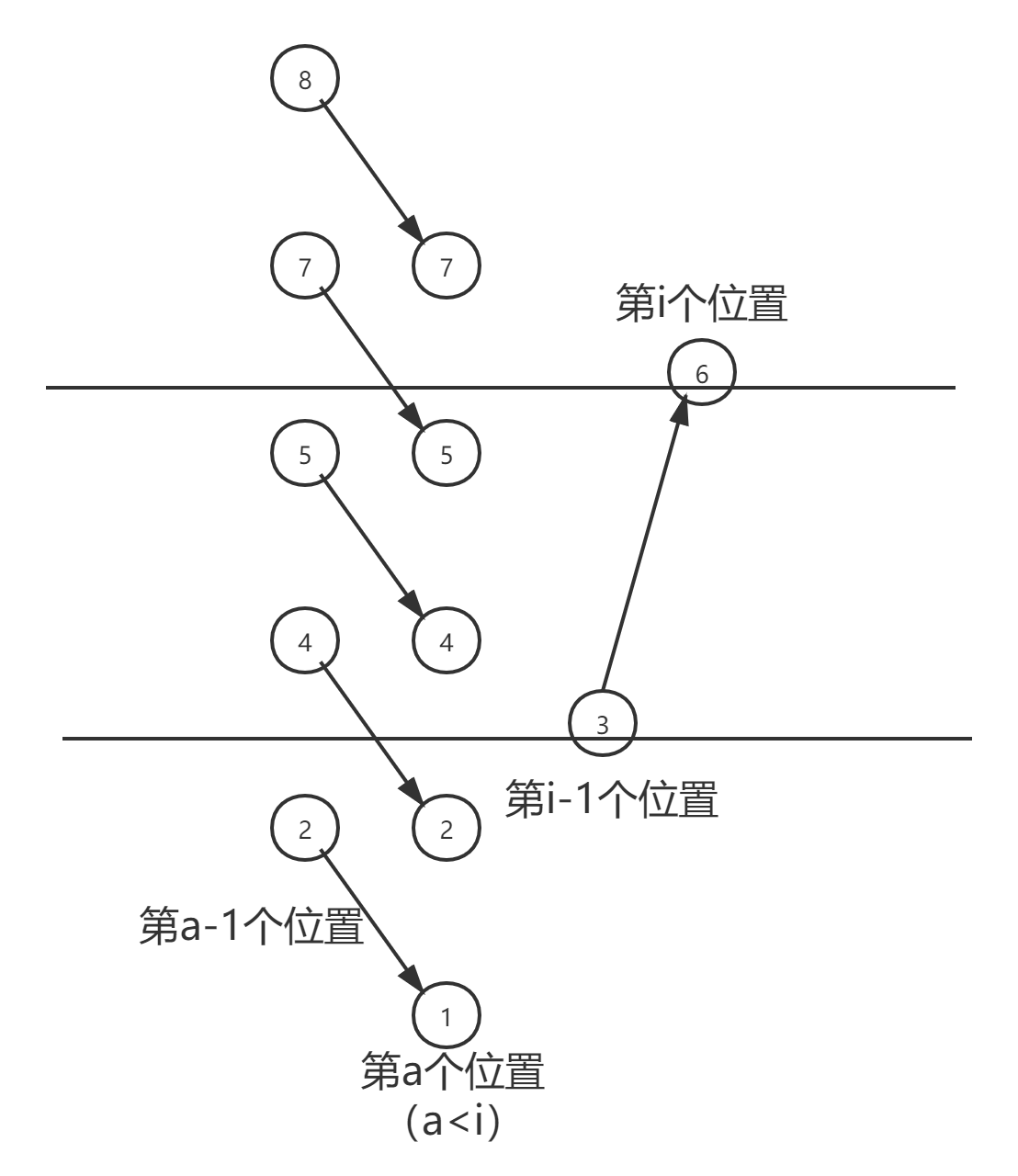
当前位置i与i-1的差值为正，无论上一个以负数差值结尾的最长子串的最后一位数字是不是位于i-1位置（图中画出了最后两个位置，即a-1位置与a位置），我们都可以通过down+1来就表示新的以正数差值结尾的最长子串的长度up，因为无论图中哪种情况（包括a与i-1位置的值相等等图中未画出情况）通过删掉a或i-1位置都可以新拼接出一个长度为down+1的以正数差值结尾的最长子串。

力扣474题 一和零

问题

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中最多有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

力扣链接：https://leetcode-cn.com/problems/ones-and-zeroes

示例

1
2
3
4
输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
1
2
3
输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

题解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        if (strs == null || strs.length <= 0) {
            return 0;
        }

        // dp[i][j] 表示 当前数组中，最多有 i个0、j个1 的组合数
        int[][] dp = new int[m + 1][n + 1];
        int oneNum;
        int zeroNum;
        for (String str : strs) {
            //记录当前字符串中0和1的数量
            oneNum = 0;
            zeroNum = 0;
			
            char[] chars = str.toCharArray();
            for (char aChar : chars) {
                if (aChar == '0') {
                    zeroNum++;
                } else {
                    oneNum++;
                }
            }

            /*
                dp[i][j] 的结果有两种情况：
                	1、当前状态(dp[i][j])
                	2、上一个状态(dp[i - zeroNum][j - oneNum])的个数 + 1
             */
            for (int i = m; i >= zeroNum; i--) {
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }

        return dp[m][n];
    }
}