图论及其应用

对于任意无向图G(输入为矩阵)，编写程序实现：

  • 任务一：画出图G，并给所有顶点和边标号
  • 任务二：求出图G的度序列
  • 任务三：画出图G的补图
  • 任务四：判断图G的连通性
  • 任务五：求出图G的边连通度和点连通度
  • 任务六：求出图G的最小点割集和最小边割集(元素最少)

解决方案

任务一（画出图G，并给所有顶点和边标号）

  • 通过 BrushTools 类中的 draw_vertex()# 画点, draw_edge()# 画边, show()# 展示绘制图像 方法实现
  • 使用二维矩阵接收点和边，点用坐标表示，边用邻接矩阵表示，如下所示：
1
2
3
4
5
6
7
8
9
import numpy as np

# 接收点
v = np.array([[1, 1], [1, 4], [7, 3], [5, 1]])
# 接收边
e = np.array([[1, 2, 0, 0],
              [2, 0, 0, 1],
              [0, 0, 0, 0],
              [0, 1, 0, 0]])
  • 使用python绘图库matplotlib实现图的绘制
    • 使用matplotlib中的 scatter(x坐标, y坐标, c="颜色") 函数绘制图的顶点
    • 使用matplotlib中的 plot(x坐标, y坐标, c="颜色") 函数绘制图的边，其中边的始点和终点坐标通过邻接矩阵e找到对应顶点坐标矩阵v中相应的坐标
    • 通过matplotlib中的 add_artist(plt.Circle((圆心坐标), 半径, fill=是否填充, color="颜色")) 函数为画布上添加圆形来表示环
    • 使用matplotlib中的 annotate(注释内容, xy=[添加注释的点的坐标], xytext=[注释文字的坐标]) 注释函数为点和边添加注释。注：在非简单无向图中，平行边通过为一条边添加多个不同的边注释来表示
    • 使用matplotlib中的 show() 函数将绘制完的图像进行展示

任务二（求出图G的度序列）

  • 通过 CalcTools 类中的 calc_degrees() 方法实现度序列的计算
  • 因为是无向图，因此点vi的度数只需要考虑邻接矩阵 e 中从vi点出发的边的条数，即关注邻接矩阵中的第i行，其中，环提供两度，该方法的主要结构如下：
1
2
3
4
5
6
7
8
9
10
11
d_line = []
d = 0
for i in range(0, self.e.shape[0]):
    for j in range(0, self.e.shape[1]):
        if self.e[i][j] > 0:
            if i == j:
                d += 2 * self.e[i][j]
            else:
                d += 1 * self.e[i][j]
    d_line.append(d)
    d = 0
  • 其中d_line用来保存最终返回的度序列，当i==j时，说明该边为环，当内层循环结束时，将该点的度数和添加到d_line中

任务三（画出图G的补图）

  • 通过 BrushTools 类中的 draw_complement 方法实现补图的计算和绘制
  • 先将原图预处理为简单图，遍历邻接矩阵 e ，将对角线数字置为0（去环），将其他非0位置的值置为1（去平行边）
1
2
3
4
5
6
7
8
9
for i in range(0, e.shape[0]):
    for j in range(0, e.shape[1]):
        # 去环
        if i == j:
            e[i][j] = 0
        else:
            # 去平行边
            if e[i][j] > 0:
                e[i][j] = 1
  • 将处理后的邻接矩阵 e 中的非对角线位置的值进行非操作，即可获得该图补图的邻接矩阵
1
2
3
4
5
6
7
for i in range(0, ec.shape[0]):
    for j in range(0, ec.shape[1]):
        if i != j:
            if ec[i][j] == 1:
                ec[i][j] = 0
            else:
                ec[i][j] = 1
  • 调用任务一中实现的绘图方法 BrushTools.show() 实现补图的绘制与展示

任务四（判断图G的连通性）

  • 通过 CalcTools 类中的 judge_connect() 方法判断图的连通性
  • 无向图中若任意两点均可达，则为连通的
  • 从图中任意一点vi出发，将该点加入连通点列表 v_connect 中，判断能否到达其他不在 v_connect 中的点，即邻接矩阵 e 的第i行是否有非零数
    • 如果没有，则说明vi与其他点不相邻，说明该图为非连通的
    • 如果有，则说明vi与对应点相邻，进行递归，重复以上过程，继续判断对应点是否能继续走到其他点？
  • 完成以上过程后，得到从vi点出发可以到达所有点的列表 v_connect ，对其进行处理，判断其中的元素个数是否与该图总顶点数相同，如果相同则说明从vi点出发可以到达所有顶点，该图连通，否则不连通
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 计算图的连通性
def calc_connect(self, flag):
    self.v_connect.append(flag)
    for i in range(0, self.e.shape[1]):
        if i > 0 and i not in self.v_connect:
            if self.e[flag][i] != 0:
                self.calc_connect(i)


# 判断连通性
def judge_connect(self):
    flag = False
    self.calc_connect(0)
    result = list(set(self.v_connect))
    self.v_connect = []
    if len(result) == self.e.shape[0]:
        flag = True
    return flag

任务五、六

  • 任务五：求出图G的边连通度和点连通度
  • 任务六：求出图G的最小点割集和最小边割集(元素最少)
  • 任务五和任务六相关，找出最小边割集/点割集，即可获取图的边连通度/点连通度
  • 该任务的整体思路为，以找出最小边割集为例，在连通图中从少到多删除图中的边，然后调用任务四中实现的判断图连通性的方法 CalcTools.judge_connect()
    或其变体CalcTools.judge_connect_complex()
    来判断删除边后的图的连通性，一旦图不连通，则找出一个图的最小边割集，该边割集的大小即为该图的边连通度，该方法的思想同样可以找出所有的最小边割集，此处实现只找出其中一个作为展示
    • 判断边连通度
      • 首先判断输入图是否为连通图 judge_connect() 非连通图直接返回空列表
      • 第一层循环为删除的边的个数，其范围为1到n-1(n为点的个数)： for num in range(1, self.e.shape[0])
        • 使用 e2del = list(combinations(待组合列表, 组合大小)) 函数来获取本次循环中要删除的边的组合，其中待组合列表为邻接矩阵 e
          中所表示的所有边，组合大小为i，即本次循环要删除的边的个数， e2del即为本次循环中要删除的边的各种组合
        • 第二层循环，从e2del中取出待删除的边，进行删除，然后判断图的连通性，如果不连通则找到其中一个最小边割集，将其进行返回，否则对邻接矩阵 e 进行复原，继续进行循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
for edges in e2del:
    del_count = 0

    cut = []

    temp_e = copy.deepcopy(self.e)
    for i in range(0, temp_e.shape[0]):
        for j in range(i + 1, temp_e.shape[1]):
            while temp_e[i][j] > 0:
                del_count += 1
                temp_e[i][j] -= 1
                temp_e[j][i] -= 1

                for e in edges:
                    # 说明该边在要删除的边组合中
                    if del_count == e:
                        self.e[i][j] = 0
                        self.e[j][i] = 0
                        # 对该边进行保存
                        cut.append((i, j))
    # 删除完边，判断图的连通性
    flag = self.judge_connect()

    # 对边进行还原
    self.e = copy.deepcopy(dc_e)

    if not flag:
        return cut
  • 计算点割集的整体思想与计算边割集的思想一致，在 CalcTools.calc_vertex_connect()
    方法中实现，该方法从少到多找出所有删除点的组合，然后对点和关联边进行删除，同时判断删除点和边之后的图的连通性，此处不再做过多解释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def calc_vertex_connect(self):
    # 深拷贝原邻接矩阵
    dc_e = copy.deepcopy(self.e)

    # 判断是不是连通图
    if not self.judge_connect():
        return []

    # 计算图中的所有点个数
    v_count = self.v.shape[0]
    # 待组合列表
    v_combination = range(0, v_count)

    # 删点和相关联的边，然后判断是否连通
    for num in range(1, self.v.shape[0]):
        # 确定要删除的点组合
        v2del = list(combinations(v_combination, num))

        # 循环删除要删除的点和边组合
        for vertexes in v2del:
            cut = []

            self.e = np.array(self.e)
            for v in vertexes:
                self.e[v, :] = 0
                self.e[:, v] = 0
                cut.append(v)

            # 如果删除的点数等于n-1，直接返回
            if num == self.v.shape[0] - 1:
                return cut

            # 删除完点和关联边，判断图的连通性
            flag = self.judge_connect_complex(self.v.shape[0], vertexes)
            if not flag:
                return cut

            # 对边进行还原
            self.e = copy.deepcopy(dc_e)
    self.e = copy.deepcopy(dc_e)

完整代码

绘图工具类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
import matplotlib.pyplot as plt
import copy


class BrushTools:
    # 创建figure
    figure = plt.figure()
    # 创建axes
    axes = figure.add_subplot(1, 1, 1)

    # 保存点坐标
    v = []
    # 保存边关系
    e = []

    def __init__(self, v, e):
        self.v = v
        self.e = e

    # 在画布上画点
    def draw_vertex(self):
        # 标点
        self.axes.scatter(self.v[:, 0], self.v[:, 1], c="red")
        # 给点加注释
        for i in range(0, self.v.shape[0]):
            self.axes.annotate("v" + str(i),
                               xy=[self.v[i, 0], self.v[i, 1]],
                               xytext=[self.v[i, 0] + 0.05, self.v[i, 1] - 0.05])

    # 在画布上画边
    def draw_edge(self):
        # 标边
        ec = copy.deepcopy(self.e)
        count = 0
        for i in range(0, ec.shape[0]):
            for j in range(0, ec.shape[1]):
                if ec[i, j] > 0:
                    # 判断是不是环
                    if i == j:
                        self.axes.add_artist(plt.Circle((self.v[i, 0], self.v[i, 1] + 0.2), 0.2,
                                                        fill=False,
                                                        color="green"))

                        # 考虑多个环的情况，加多个注释
                        a_str = ""
                        for k in range(0, ec[i][j]):
                            a_str = a_str + "e" + str(count) + ","
                            count += 1

                        self.axes.annotate(a_str[:-1],
                                           xy=[self.v[i, 0] + 0.15, self.v[i, 1] + 0.3],
                                           xytext=[self.v[i, 0] + 0.15, self.v[i, 1] + 0.3])

                    else:
                        ec[j, i] = 0
                        x = [self.v[i, 0], self.v[j, 0]]
                        y = [self.v[i, 1], self.v[j, 1]]
                        self.axes.plot(x, y, c="green")

                        # 给边加注释(考虑平行边的情况)
                        a_str = ""
                        for k in range(0, ec[i][j]):
                            a_str = a_str + "e" + str(count) + ","
                            count += 1

                        xm = (self.v[i, 0] + self.v[j, 0]) / 2
                        ym = (self.v[i, 1] + self.v[j, 1]) / 2
                        self.axes.annotate(a_str[:-1], xy=[xm, ym], xytext=[xm + 0.02, ym + 0.02])

    # 画出图的补图（考虑简单无向图）
    def draw_complement(self):
        # 预处理，确保是简单无向图
        ec = copy.deepcopy(self.e)
        ec = self.transform2simple(ec)

        # 生成补图
        for i in range(0, ec.shape[0]):
            for j in range(0, ec.shape[1]):
                if i != j:
                    if ec[i][j] == 1:
                        ec[i][j] = 0
                    else:
                        ec[i][j] = 1

        # 画出补图
        e_temp = copy.deepcopy(self.e)
        self.e = ec
        self.show()
        self.e = e_temp

    # 将无向图转换为简单无向图(去环，去平行边)
    def transform2simple(self, e):
        for i in range(0, e.shape[0]):
            for j in range(0, e.shape[1]):
                # 去环
                if i == j:
                    e[i][j] = 0
                else:
                    # 去平行边
                    if e[i][j] > 0:
                        e[i][j] = 1
        return e

    def show(self):
        self.axes.cla()
        self.draw_vertex()
        self.draw_edge()

        plt.axis('scaled')
        self.figure.show()

图计算工具类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
import copy
from itertools import *

import numpy as np


class CalcTools:
    # 保存点坐标
    v = []
    # 保存边关系
    e = []

    # 临时变量
    v_connect = []

    def __init__(self, v, e):
        self.v = v
        self.e = e

    # 计算图的度序列
    def calc_degrees(self):
        d_line = []
        d = 0
        for i in range(0, self.e.shape[0]):
            for j in range(0, self.e.shape[1]):
                if self.e[i][j] > 0:
                    if i == j:
                        d += 2 * self.e[i][j]
                    else:
                        d += 1 * self.e[i][j]
            d_line.append(d)
            d = 0
        # print("任务二：图的度序列为" + str(d_line))
        return d_line

    # 计算图的连通性
    def calc_connect(self, flag):
        self.v_connect.append(flag)
        for i in range(0, self.e.shape[1]):
            if i > 0 and i not in self.v_connect:
                if self.e[flag][i] != 0:
                    self.calc_connect(i)

    # 判断连通性
    def judge_connect(self):
        flag = False
        self.calc_connect(0)
        result = list(set(self.v_connect))
        self.v_connect = []
        if len(result) == self.e.shape[0]:
            # print("任务四：该无向图是连通的")
            flag = True
        else:
            # print("任务四：该图只有" + str(len(result)) + "个点是连通的，分别是" + str(result))
            # print("任务四：该无向图是不连通的")
            flag = False
        return flag

    # 判断连通性
    def judge_connect_complex(self, v_size, del_v):
        flag = False
        for i in range(0, v_size):
            if i not in del_v:
                # print(i)
                self.calc_connect(i)
                break

        result = list(set(self.v_connect))
        self.v_connect = []

        if len(result) == v_size - len(del_v):
            # print(v_size - len(del_v))
            # print("任务四：该无向图是连通的")
            flag = True
        else:
            # print("任务四：该图只有" + str(len(result)) + "个点是连通的，分别是" + str(result))
            # print("任务四：该无向图是不连通的")
            flag = False
        return flag

    # 计算边连通度
    def calc_edge_connect(self):
        # 深拷贝原邻接矩阵
        dc_e = copy.deepcopy(self.e)

        # 判断是不是连通图
        if not self.judge_connect():
            return []

        # 计算图中的所有边数
        e_count = 0
        for i in range(0, self.e.shape[0]):
            for j in range(0, self.e.shape[1]):
                e_count = e_count + self.e[i][j]
        e_count = int(e_count / 2.0)
        # print("总边数" + str(e_count))

        e_combination = range(1, e_count + 1)

        # 删边，然后判断是否连通
        for num in range(1, self.e.shape[0]):

            # 确定要删除的边组合
            e2del = list(combinations(e_combination, num))
            # print(e2del)
            # 循环删除要删除的边组合
            for edges in e2del:
                del_count = 0

                cut = []

                temp_e = copy.deepcopy(self.e)
                for i in range(0, temp_e.shape[0]):
                    for j in range(i + 1, temp_e.shape[1]):
                        while temp_e[i][j] > 0:
                            del_count += 1
                            temp_e[i][j] -= 1
                            temp_e[j][i] -= 1

                            for e in edges:
                                # 说明该边在要删除的边组合中
                                if del_count == e:
                                    self.e[i][j] = 0
                                    self.e[j][i] = 0
                                    # print(str(self.e))
                                    # 对该边进行保存
                                    cut.append((i, j))
                # 删除完边，判断图的连通性
                # print("测试连通性" + "\n" + str(self.e))

                flag = self.judge_connect()

                # 对边进行还原
                self.e = copy.deepcopy(dc_e)

                if not flag:
                    return cut

        self.e = copy.deepcopy(dc_e)

    # 计算点连通度
    def calc_vertex_connect(self):

        # 深拷贝原邻接矩阵
        dc_e = copy.deepcopy(self.e)

        # 判断是不是连通图
        if not self.judge_connect():
            return []

        # 计算图中的所有点个数
        v_count = self.v.shape[0]
        # print("总点数" + str(v_count))

        v_combination = range(0, v_count)

        # 删点和相关联的边，然后判断是否连通
        for num in range(1, self.v.shape[0]):

            # 确定要删除的点组合
            v2del = list(combinations(v_combination, num))
            # print(v2del)

            # 循环删除要删除的点和边组合
            for vertexes in v2del:
                del_count = 0

                cut = []

                # print(vertexes)

                self.e = np.array(self.e)
                for v in vertexes:
                    self.e[v, :] = 0
                    self.e[:, v] = 0
                    cut.append(v)

                # 删除完点和关联边，判断图的连通性
                # print("测试连通性" + "\n" + str(self.e))

                if num == self.v.shape[0] - 1:
                    return cut

                flag = self.judge_connect_complex(self.v.shape[0], vertexes)

                if not flag:
                    return cut

                # 对边进行还原
                self.e = copy.deepcopy(dc_e)

            # print("===================================")

        self.e = copy.deepcopy(dc_e)

主函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import numpy as np
from brush_tools import BrushTools
from calculate_tools import CalcTools

if __name__ == '__main__':
    # # 接收点
    # v = np.array([[1, 1], [1, 4], [7, 3], [5, 1]])
    # # 接收边
    # e = np.array([[1, 2, 0, 0],
    #               [2, 0, 0, 1],
    #               [0, 0, 0, 0],
    #               [0, 1, 0, 0]])

    # # 接收点
    # v = np.array([[1, 1], [1, 3], [2, 2], [3, 2]])
    # # 接收边
    # e = np.array([[0, 1, 1, 0],
    #               [1, 0, 1, 0],
    #               [1, 1, 1, 1],
    #               [0, 0, 1, 0]])

    # 接收点
    v = np.array([[1, 1], [1, 3], [3, 1], [3, 3], [5, 2], [7, 1], [7, 3], [9, 1], [9, 3]])
    # 接收边
    e = np.array([[0, 1, 1, 1, 0, 0, 0, 0, 0],
                  [1, 0, 1, 1, 0, 0, 0, 0, 0],
                  [1, 1, 0, 1, 1, 0, 0, 0, 0],
                  [1, 1, 1, 0, 1, 0, 0, 0, 0],
                  [0, 0, 1, 1, 0, 1, 1, 0, 0],
                  [0, 0, 0, 0, 1, 0, 1, 1, 1],
                  [0, 0, 0, 0, 1, 1, 0, 1, 1],
                  [0, 0, 0, 0, 0, 1, 1, 0, 1],
                  [0, 0, 0, 0, 0, 1, 1, 1, 0]
                  ])

    # 任务一：画出图G，并给所有顶点和边标号
    brush = BrushTools(v, e)
    brush.show()
    print("任务一：如图所示")

    # 任务二：求出图G的度序列
    calc = CalcTools(v, e)
    degrees = calc.calc_degrees()
    print("任务二：图的度序列为" + str(degrees))

    # 任务三：画出图G的补图
    brush.draw_complement()
    print("任务三：如图所示，原图已被处理为简单无向图")

    # 任务四：连通性
    calc = CalcTools(v, e)
    flag = calc.judge_connect()
    print("任务四：该图的连通性为" + str(flag))

    # 任务五：求边连通度和点连通度
    calc = CalcTools(v, e)
    e_cut_set = calc.calc_edge_connect()
    print("任务五、六：边连通度是" + str(len(e_cut_set)) + ",最小边割集是" + str(e_cut_set))

    v_cut_set = calc.calc_vertex_connect()
    print("任务五、六：点连通度是" + str(len(v_cut_set)) + ",最小点割集是" + str(v_cut_set))

测试结果

任务一

  • 画出图G，并给所有顶点和边标号
  • 输入点和边如下所示：
1
2
3
4
5
v = np.array([[1, 1], [1, 4], [7, 3], [5, 1]])
e = np.array([[1, 2, 0, 0],
              [2, 0, 0, 1],
              [0, 0, 0, 0],
              [0, 1, 0, 0]])
  • 绘图结果展示：

任务一

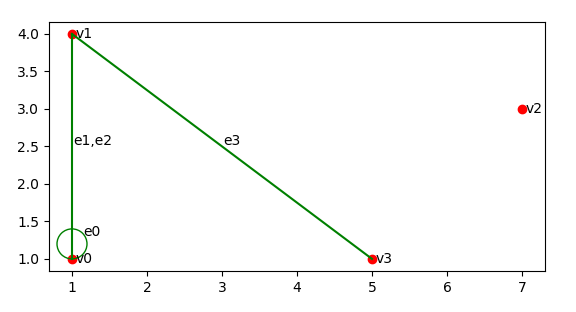
任务二

  • 求出图G的度序列
  • 输入点和边与任务一相同，度序列如下，与任务一展示图结果相对应，注：图中e1和e2为平行边
1
# 任务二：图的度序列为[4, 3, 0, 1]

任务三

  • 画出图G的补图
  • 输入点和边与任务一相同，补图如下所示，与任务一的结果相对应

任务三

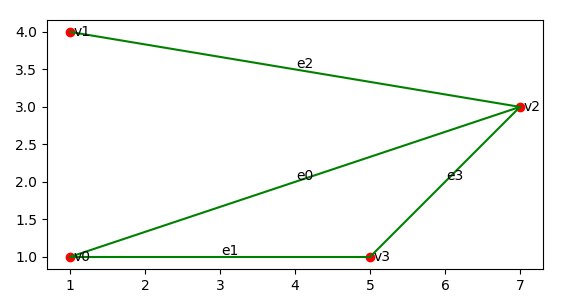
任务四

  • 判断图G的连通性
  • 输入点和边与任务一相同，运行方法判断图的连通性，结果如下所示：
1
# 任务四：该图的连通性为False
  • 重新输入新的点坐标和边邻接矩阵，使新的图连通，如下所示
1
2
3
4
5
6
7
# 接收点
v = np.array([[1, 1], [1, 3], [2, 2], [3, 2]])
# 接收边
e = np.array([[0, 1, 1, 0],
              [1, 0, 1, 0],
              [1, 1, 1, 1],
              [0, 0, 1, 0]])
  • 重新输入图的展示与连通性判断结果如下：

任务四

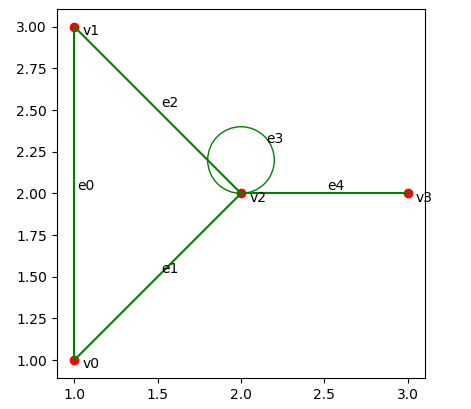
1
# 任务四：该图的连通性为True

任务五、六

  • 求出图G的边连通度和点连通度
  • 求出图G的最小点割集和最小边割集(元素最少)
  • 输入的图如下所示：
1
2
3
4
5
6
7
8
9
10
11
12
13
# 接收点
v = np.array([[1, 1], [1, 3], [3, 1], [3, 3], [5, 2], [7, 1], [7, 3], [9, 1], [9, 3]])
# 接收边
e = np.array([[0, 1, 1, 1, 0, 0, 0, 0, 0],
              [1, 0, 1, 1, 0, 0, 0, 0, 0],
              [1, 1, 0, 1, 1, 0, 0, 0, 0],
              [1, 1, 1, 0, 1, 0, 0, 0, 0],
              [0, 0, 1, 1, 0, 1, 1, 0, 0],
              [0, 0, 0, 0, 1, 0, 1, 1, 1],
              [0, 0, 0, 0, 1, 1, 0, 1, 1],
              [0, 0, 0, 0, 0, 1, 1, 0, 1],
              [0, 0, 0, 0, 0, 1, 1, 1, 0]
              ])

任务五

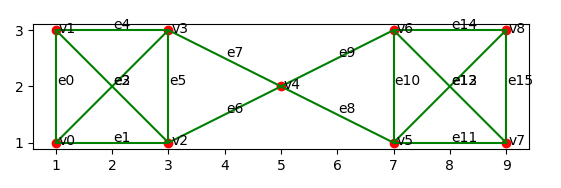
  • 边割集/点割集，边连通度/点连通度计算结果如下：
1
2
# 任务五、六：边连通度是2,最小边割集是[(2, 4), (3, 4)]
# 任务五、六：点连通度是1,最小点割集是[4]
  • 其中边割集(2,4)表示从点v2到v4的边，即图中的e6，同理(3,4)表示图中的e7
  • 点割集中的4表示图中的v4