匈牙利算法

匈牙利算法步骤

  1. 任给初始匹配M
  2. 若M饱和V1则结束，否则转(3)
  3. 在V1中找一个非M饱和点x，置S={x}，T={ }
  4. 若N(S)=T，则停止，否则在N(S)-T中任选一点y
  5. 若y为M饱和点转(6)，否则求一条从x到y的M可增广路P，并更新匹配M，转(2)
  6. 因为y是M饱和点，所以M中有一边(y，u)，置S=S∪{u}，T=T∪{y}，转(4)

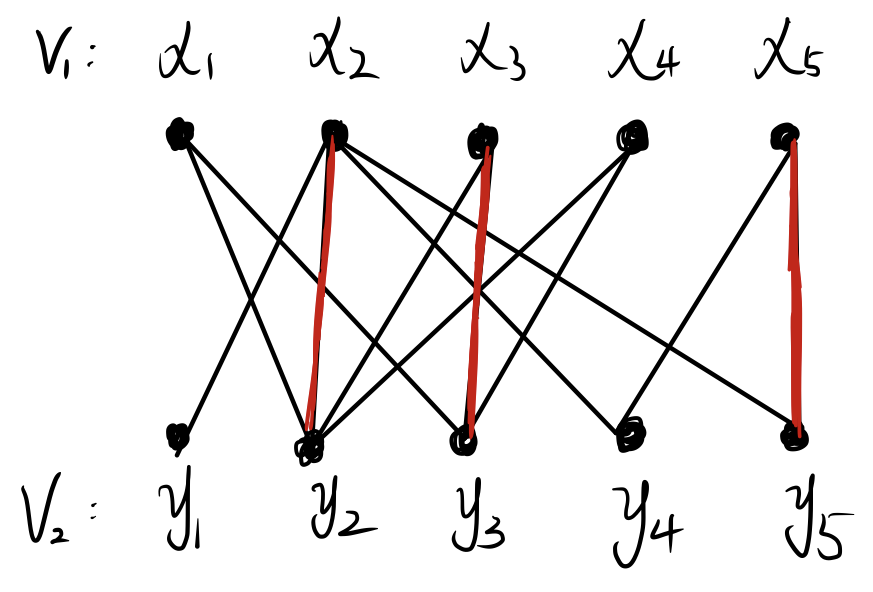
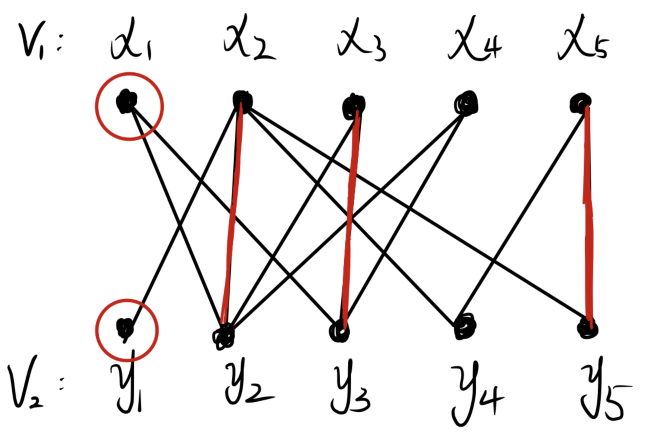
代码部分

输入二部图如下：

可以由以下代码表示：

1
2
3
4
5
6
# 输入二部图
bi_graph = [[0, 1, 1, 0, 0],
            [1, 1, 0, 1, 1],
            [0, 1, 1, 0, 0],
            [0, 1, 1, 0, 0],
            [0, 0, 0, 1, 1]]

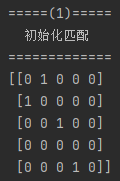
(1). 任给初始匹配M

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 初始化匹配
def init_matching(graph):
    x, y = np.shape(graph)

    matching = np.zeros((x, y), int)

    matched = []

    for i in range(0, x):
        for j in range(0, y):
            if graph[i][j] == 1 and j not in matched:
                matching[i][j] = 1
                matched.append(j)
                break

    return matching

创建一个与二部图矩阵对应的匹配矩阵，初始化匹配矩阵的规则是：遍历输入的二部图矩阵，从V1出发找到V2找边，如果该边在V2中饱和的点已经在匹配中出现，则不选择该边，当找到一条合适的边时，将其加入匹配矩阵结束本次循环，并在V1中找到下一个点继续重复以上过程。

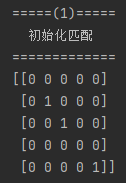
以上过程结束后即可获得如下(a)所示初始匹配矩阵。由于此初始化方法在本例中直接给出了最大匹配，无法体现完整的算法过程，因此在之后的代码中将采用(b)作为初始匹配。

(a)

(b)

(b)初始化匹配结果如图所示：

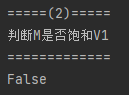
(2). 判断匹配M是否饱和V1

1
2
3
4
5
6
7
8
# 判断匹配是否饱和所有V1点
def judge_saturated(matching):
    saturate = np.sum(matching, axis=1)
    for i in saturate:
        if i == 0:
            return False

    return True

将匹配矩阵按维度求和，只要有一行的和等于0则M未饱和V1。如果饱和则当前匹配为最大匹配，直接输出结果，否则转到(3)。

1
2
3
4
5
6
if judge_saturated(matching):
    # 若M饱和V1，则M为最大匹配
    print("=====(结束)=====")
    print("最大匹配:")
    print(matching)
    return matching

该案例的饱和结果如下：

(3). 在V1中找一个非M饱和点x，置S={x}，T={ }

1
2
3
4
5
6
7
8
9
10
11
# 初始化S和T
def init_s_and_t(matching):
    s = []
    t = []
    saturate = np.sum(matching, axis=1)
    for i in range(0, len(saturate)):
        if saturate[i] == 0:
            s.append(i)
            break

    return s, t

将匹配矩阵按维度求和，值为0的行对应的V1中的点即为非M饱和点，取该点为x，初始化S={x}，T={ }。

(4). 如果N(S)=T，则停止。否则选择y属于N(S)-T

(4.1). 获得N(S) 判断N(S)与T是否相等

1
2
3
4
5
6
7
8
9
10
11
12
# 获得N(S)
def get_neighbor(graph, s):
    x, y = np.shape(graph)
    neighbor = []

    for i in s:
        for j in range(0, y):
            if graph[i][j] != 0 and j not in neighbor:
                neighbor.append(j)

    neighbor.sort()
    return neighbor

在二部图矩阵中，从每行出发找非零值对应的V2中的点即为该点相邻的点，找出S中的点对应的所有点即可获得N(S)的值。

1
2
3
4
5
if np.all(neighbor == t):
    print("=====(结束)=====")
    print("最大匹配:")
    print(matching)
    return matching

如果相等则当前匹配为最大匹配，直接输出结果。

(4.2). 初始化y

否则初始化y∈N(S)-T

1
2
n_minus_t = [i for i in neighbor if i not in t]
y = n_minus_t[0]

在本案例中：

(5.1). 判断y是否为M饱和点

1
2
3
4
5
6
7
# 判断该点是否是饱和点
def if_be_saturated(y, matching):
    saturate_y = np.sum(matching, axis=1)
    if saturate_y[y] == 1:
        return True

    return False

如果不是饱和点则求一条从x到y的M可增广路P，并更新匹配M，转(2)；如果是饱和点则转到(6)。

在本案例中：

(6). 因为y是M饱和点，所以M中有一边(y，u)，找到u，置S=S∪{u}，T=T∪{y}，转(4)。

在本案例中，之后的过程为：

(5.2) 求一条从x到y的M可增广路P，并更新匹配M, 转(2)

经过以上过程找到非饱和点y，此时x与y如图所示，需要找到一条从x到y的可增广路。

1
2
3
4
5
6
7
# 寻找可增广路
def find_augmentative_path(graph, matching, x, y):
    # 从V1到V2所有可以走的非M边
    path = v1_to_v2(graph, matching, x, [], y)
    path = path[:-1]
    # 可增广路
    return path

经过前面的算法处理，现阶段一定可以找到一个从x到y的可增广路。该路开始于x点，终止与y点。该路径中V1和V2部分的点交替出现，从V1到V2的边不在匹配M中，可以有多条，从V2到V1的边在匹配M中，只能有一条。可能找到多条可增广路，不影响最后结果的正确性。交错路以走到y点标志结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 从V1到V2找一条非M边
def v1_to_v2(graph, matching, x, path, goal):
    a_path = []

    gx, gy = np.shape(graph)
    for ggy in range(0, gy):
        if graph[x][ggy] == 1:

            # 防止重复走同一个点
            if if_y_in_path(ggy, path):
                continue

            # 如果走到y则结束
            if ggy == goal:
                a_path = path.copy()
                a_path.append([x, ggy])
                a_path.append([gx, gy])
                break

            new_path = path.copy()
            new_path.append([x, ggy])

            v2v1 = v2_to_v1(graph, matching, ggy, new_path, goal)

            if len(v2v1) > 0:
                a_path = v2v1

            # 如果走到y则结束
            len_of = len(v2v1) - 1
            if v2v1[len_of][0] == gx:
                return a_path

    return a_path

从V1到V2找一条非M边的代码如上所示，graph为二部图矩阵，matching为匹配矩阵，x为本次的出发点，path保存已经走过的交错路，goal记录最终结束的点。

从graph矩阵中找出从x出发所有可以走到的V2中的点，进行判断。

如果该点已经在交错路path中出现过了，则跳过该点，因为可增广路中无重复的边，而从V2中出发的边只能走M中的边，每个点最多只有一条，因此V2中的点在本算法path中只能出现一次。

1
2
3
4
5
6
7
# 判断v2中的点是否已在路径中
def if_y_in_path(y, path):
    for p in path:
        if path[1] == y:
            return True

    return False

如果该点走到了y点（即与goal的值相同），说明找到了一条可增广路，将该点加入到path中，并在path的最后加上标记（a_path.append([gx, gy])）以结束该算法。

如果以上条件均不满足，则将该点加入path中，并将二部图(graph)、匹配矩阵(matching)、该V2中的点(y)、目前找到的交错路（path）、结束目标(goal)作为参数，传入v2_to_v1()方法中，以继续找到一条从V2到V1的匹配边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 从V2到V1找一条M边
def v2_to_v1(graph, matching, y, path, goal):
    a_path = []

    mx, my = np.shape(matching)
    for mmx in range(0, mx):
        if matching[mmx][y] == 1:
            new_path = path.copy()
            new_path.append([mmx, y])

            v1v2 = v1_to_v2(graph, matching, mmx, new_path, goal)

            if len(v1v2) > 0:
                a_path = v1v2

            len_of = len(v1v2) - 1
            if v1v2[len_of][0] == mx:
                return a_path

    return a_path

v2_to_v1与v1_to_v2方法相似，因为V2到V1找的是匹配边，因此不用考虑结束值和重复值的问题。

两种方法互相调用，v1_to_v2找从V1到V2的非M边，v2_to_v1找从V2到V1的M边。在两个方法的调用过程中如果出现一条死路，该方法将返回一个空表，这种情况下该空表会随着调用关系向外传递，使调用该方法的方法忽略这条路径。最终调用关系将在v1_to_v2找到y之后结束，该方法在找到y之后会在path的最后添加标记并返回，在v1_to_v2和v2_to_v1都对path最后的标记进行了检查，当检查出该标记后直接返回不再进行后续过程。

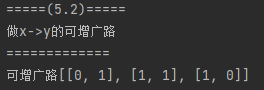
根据以上思路，在本例中找到的可增广路为：

(5.3). 根据可增广路更新匹配，转(2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def update_matching(path, matching):
    flag = True
    for p in path:
        if flag:
            matching[p[0]][p[1]] = 1
            flag = False
            continue

        if not flag:
            matching[p[0]][p[1]] = 0
            flag = True
            continue

    return matching

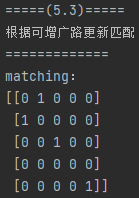
根据可增广路交替更新匹配中的边。

在本案例中，更新后匹配结果如下图所示：

之后代码转至(2)，继续重复上述过程，直到达到结束条件，输入最大匹配。

代码的完整运行结果如下图所示：