暗通道先验去雾

• He Kaiming, Sun Jian and Tang Xiaoou. Single Image Haze Removal Using Dark Channel Prior. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 12, pp. 2341-2353, Dec. 2011, doi: 10.1109/TPAMI.2010.168. [暗通道先验 Dark Channel Prior]
• He Kaiming, Sun Jian and Tang Xiaoou. Guided Image Filtering. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 6, pp. 1397-1409, June 2013, doi: 10.1109/TPAMI.2012.213. [引导滤波 Guided Filtering]

理论基础

大气散射模型

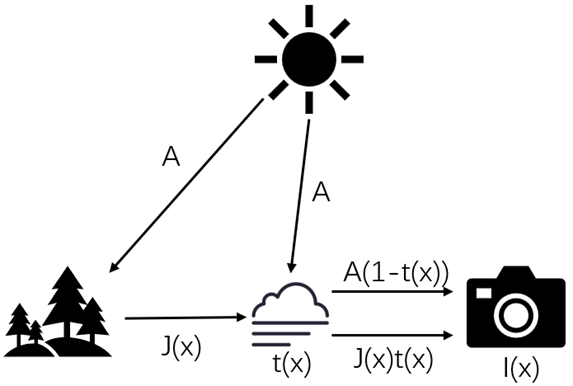
传统去雾方法对雾天成像过程进行物理建模，通过求解模型的未知量进而恢复清晰图像。经典的大气散射模型如图1所示，它假设成像时接收到的光源主要来自两个部分：一是场景中的物体反射场景光源$A$形成的反射光$J(x)$经过雾颗粒的衰减影响$t(x)$到达相机的部分$J(x)t(x)$，这部分是对成像质量的直接影响；二是雾颗粒对场景光源$A$散射影响$1-t(x)$后的散射光到达相机的部分$A(1-t(x))$。设备接收到这两部分的光，形成最后的降质雾图像$I(x)$，根据以上结果即可得到雾形成过程的物理建模，如式(1)所示：

$$I(x)=J(x)t(x)+A(1-t(x)) \tag 1$$

根据以上建模，在去雾的过程中，只要能从雾图像$I(x)$中估计出场景光源强度$𝐴$和透射率$𝑡(𝑥)$，即可代入式(1)求解无雾图像$J(x)$。然而建模中存在多个未知量，属于不适定问题，需要借助先验知识加以约束，缩小解空间。

暗通道先验

暗通道先验是去雾领域的重要先验知识，是基于统计学观测结果而做出的先验性假设，通过领域内通用知识的引入协助物理模型未知量的求解。

如图2所示，何恺明等人观测到，在大部分无雾图像任一像素点对应的三个通道中，总有一个通道的像素值很小且接近于0（如图2(a)(b)所示，将无雾图像(a)中每个像素点在三个通道中的最小值提取出来得到暗通道图(b)，暗通道图的绝大部分像素点具有接近于0的像素值）；而在雾图像中，由于雾颗粒的散射光附加到对应像素点上使得像素点的三通道像素值增大，进而提取到的像素最小值一般远大于0（如图2(c)所示，雾图像中存在雾的区域像素的三通道值较大，因此提取出的暗通道图相比于无雾图像具有更大和更加明显的白色区域）。

根据观测结果提出了以下先验假设：在大部分无雾图像的非天空区域，某一区域的像素中至少存在一个像素的某一颜色通道存在非常低的亮度值，这个亮度值几乎等同于0。因此，对于一个清晰的观测图像$𝐽(x)$，其暗通道$J_{dark}(x)$可以有如下式(2)表示：

$$J_{dark}(x)=\min\limits_{y∈Ω(x)}[\min\limits_{c∈\{r,g,b\}}J^{c}(y)] \tag 2$$

其中，$𝛺(𝑥)$表示以$𝑥$为中心的一个窗口,$J^{c}$表示彩色图像对应 RGB 通道。如果$𝐽$是室外无雾图像，除了天空区域之外，$𝐽$的暗通道$J_{dark}$的强度较低并且趋于零($J_{dark}(x)=0$)。这样的观测结果称之为暗通道先验。

去雾方法

全局大气光的估算（$A$）

• 传统方法直接选取雾图像中的亮度值最高的点作为全局大气光值（场景光源的强度），这样原始雾图像中的白色物体会对此有影响，使选取的大气光值偏高。
• 暗通道的运算可以抹去原始图像中小块的白色物体（提取窗口内的最小值，可以忽略一些比窗口小的白色物体较大的像素值），所以这样估计的全局大气光值会更准确。

借助于暗通道图来从雾图像中获取$A$值：

1. 从暗通道图中按照亮度的大小选取前0.1%的像素，并记录其在图像中的位置。

2. 在原始雾图像$I(x)$中寻找这些位置上具有最高亮度的点的值，作为$A$值的估计。

透射率的估算（$t(x)$）

对式(1)大气散射模型经过变换可以得到式(3)

$$\frac{I(x)}{A}=t(x)\frac{J(x)}{A}+1-t(x) \tag 3$$

其中大气光强度$A$和雾图像$I(x)$的值已知，清晰图像$J(x)$和透射率$t(x)$未知， 假设每个窗口的透射率$𝑡(𝑥)$是相同的，为常数$\tilde{t}(x)$，且$𝐴$的值已知，对式(3)两边同时计算暗通道（式(2)），即可得到式(4)：

$$\frac{1}{A}\min\limits_{y∈Ω(x)}[\min\limits_{c∈\{r,g,b\}}I^{c}(y)]=\frac{\widetilde{t}(x)}{A}\min\limits_{y∈Ω(x)}[\min\limits_{c∈\{r,g,b\}}J^{c}(y)]+1-\widetilde{t}(x) \tag 4$$

式(4)中，$Ω(x)$代表以$x$点为中心的一个窗口，$y$是该窗口中的任一值，$c$表示图像的 RGB 通道。上式表示在图像中一个窗口区域覆盖的三个通道区域中，取像素值最小的一个点，由暗通道先验可知：

$$J_{dark}(x)\approx0,I_{dark}(x)\neq0 \tag 5$$

即在清晰图像上取暗通道图$J_{dark}(x)$得到的是一张值全部近似为0的全黑的图，而在雾图像上取暗通道图$I_{dark}(x)$通常得到的不是一张全黑的图，即其值不全部近似为0。将该先验知识加入到式(4)中，即可排除未知量$J$相关项，此时式中只有透射率$t(x)$一个未知量，即可对透射率$t(x)$进行求解。

$$\widetilde{t}(x)=1-\frac{1}{A}\min\limits_{y∈Ω(x)}[\min\limits_{c∈\{r,g,b\}}I^{c}(y)]=1-\frac{I_{dark}}{A} \tag 6$$

利用式(6)，即可通过在雾图像上取暗通道图从而求出某一窗口下的透过率值大小$\widetilde{t}(x)$，最终就可获取整张雾图像的透过率图$t(x)$。

在现实中即使是晴天，看远处的物体还是能感觉到雾的影响；另外，雾的存在让人类感到景深的存在。可以通过引入因子$ω$来控制去雾程度，1为完全去雾，0为不去雾。

$$\widetilde{t}(x)=1-\omega\frac{I_{dark}}{A} \tag 6$$

获取大气光$A$和透射率$t(x)$后，经过模型（式(1)）计算即可获取去雾图像$J(x)$:

$$J(x)=\frac{I(x)-A}{t(x)}+A \tag 7$$

代码

import cv2
import math
import numpy as np


# 提取暗通道图
def dark_channel(img, kernel_size):
    b, g, r = cv2.split(img)  # 计算三通道中的最小值
    dc = cv2.min(cv2.min(r, g), b)
    kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (kernel_size, kernel_size))
    dc_erode = cv2.erode(dc, kernel)  # 将像素值替换为其窗口邻域中的最小值
    return dc_erode


# 估计大气光A
def atm_light(img, dc):
    [h, w] = img.shape[:2]
    img_size = h * w
    num_pix = int(max(math.floor(img_size / 1000), 1))  # 需要提取的像素数量(0.1%)

    dc_vec = dc.reshape(img_size)
    im_vec = img.reshape(img_size, 3)

    indices = dc_vec.argsort()  # 升序排序并返回索引
    indices = indices[img_size - num_pix::]  # 提取出最亮的num_pix个像素的位置

    atm_sum = np.zeros([1, 3])
    for ind in range(1, num_pix):
        atm_sum = atm_sum + im_vec[indices[ind]]  # 从对应位置取出原图像中的像素值

    a = atm_sum / num_pix
    return a


# 估计透射率图t(x)
def transmission_estimate(img, a, kernel_size):
    omega = 0.95  # 去雾因子，控制去雾程度
    img_div_a = np.empty(img.shape, img.dtype)

    # t(x) = 1 - ω * I_dark / a
    for ind in range(0, 3):
        img_div_a[:, :, ind] = img[:, :, ind] / a[0, ind]
    transmission = 1 - omega * dark_channel(img=img_div_a, kernel_size=kernel_size)

    return transmission


# 引导滤波
def guided_filter(img, p, kernel_size, eps):
    # i和p的均值平滑
    mean_i = cv2.boxFilter(img, cv2.CV_64F, (kernel_size, kernel_size))
    mean_p = cv2.boxFilter(p, cv2.CV_64F, (kernel_size, kernel_size))
    # i*p的均值平滑
    mean_ip = cv2.boxFilter(img * p, cv2.CV_64F, (kernel_size, kernel_size))
    # 协方差
    cov_ip = mean_ip - mean_i * mean_p
    # i*i的均值平滑
    mean_ii = cv2.boxFilter(img * img, cv2.CV_64F, (kernel_size, kernel_size))
    # 方差
    var_i = mean_ii - mean_i * mean_i

    a = cov_ip / (var_i + eps)
    b = mean_p - a * mean_i

    # 对a和b进行均值平滑
    mean_a = cv2.boxFilter(a, cv2.CV_64F, (kernel_size, kernel_size))
    mean_b = cv2.boxFilter(b, cv2.CV_64F, (kernel_size, kernel_size))

    filtered = mean_a * img + mean_b
    return filtered


# 改善透射率图t(x)
# 窗口提取暗通道时，窗口尺寸过大会在透射率图中出现明显的矩形区域
# 通过引导滤波平滑t(x),使其区域的过渡更加平滑
def transmission_refine(img, t, kernel_size=60, eps=0.0001):
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    gray = np.float64(gray) / 255
    refined = guided_filter(img=gray, p=t, kernel_size=kernel_size, eps=eps)
    return refined


# 代入模型求解清晰图像
# J(x) = (I(x) - A) / t(x) + A
def recover(img, t, a, tx=0.1):
    res = np.empty(img.shape, img.dtype)
    t = cv2.max(t, tx)
    for ind in range(0, 3):
        res[:, :, ind] = (img[:, :, ind] - a[0, ind]) / t + a[0, ind]
    return res


if __name__ == '__main__':
    src = cv2.imread('./img/in.png')

    img = src.astype('float64') / 255
    dark = dark_channel(img=img, kernel_size=15)
    a = atm_light(img=img, dc=dark)
    t = transmission_estimate(img=img, a=a, kernel_size=15)
    t_refine = transmission_refine(img=src, t=t, kernel_size=120, eps=0.0001)
    j = recover(img, t_refine, a, 0.1)

    cv2.imwrite("./img/dark.png", dark * 255)
    cv2.imwrite("./img/t.png", t * 255)
    cv2.imwrite("./img/t_refine.png", t_refine * 255)
    cv2.imwrite("./img/J.png", j * 255)
    cv2.waitKey()

总结

部分优点

• 方法简单、体量较轻。
• 处理薄雾图像时效果比较理想。
• 受到物理模型和规律性先验知识的约束，某种程度上具有较强的鲁棒性，出现意料之外错误的可能性较低。

部分缺点

• 主要适用于雾图像中的颜色恢复，对于造成遮挡的浓雾难以增强浓雾区域模糊的细节。
• 先验知识无法覆盖所有场景，易将天空区域、场景中的白色物体等识别成雾。
• 需要一定程度的调参，参数的调整对于结果的好坏有重要影响。
• 基于大气散射模型，模型本身就强制假设雾霾分布均匀，透射率的散射系数被认为在不同空间位置上是一致的，然而空气中的雾颗粒分布是不均匀的，真实场景雾霾分布的随机性较强。

暗通道先验在传统去雾算法中非常具有代表性。传统方法的优势在于可靠性高，因为得到的解是基于物理模型的，即使出现噪声放大和颜色畸变也是在解空间内的。劣势也在于此，物理模型是基于很多理想假设的，所以当假设失效时方法也就失效了（此时解空间内不存在理想解）。暗通道先验去雾（DCP）的优越性并不仅仅在于它的简洁有效性，更在于它揭示的是对于自然图像（无雾）的统计规律，如何找到更鲁棒更有效的图像先验和更精确的雾天成像建模是这个领域中的一个重要研究方向。